√70以上 正四 角錐 体積 243664

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

正四面体の内接球の半径 この公式の応用例として，1辺が a a a の正四面体の内接球の半径を求めてみます。入試問題で頻出です。 正四面体の表面積と体積は公式として覚えておくとよいでしょう。 →正三角形の面積，正四面体の体積問題の立体を各方向から見ると下記のようになっています。 そこで、平面ABDで切った断面をCのほうから見たものを図1、 また、平面ACEで立体を2分割したものを図2とします。 Cを通りDAに平行に引いた直線とBRの交点をS、およびRからACに下ろした垂線の足をHとします。

正四 角錐 体積

正四 角錐 体積-正三角形ピラミッドの体積は、正三角形の面積の積の3分の1、つまり底辺S （ABC） 高さh （OS） ここで： Vはピラミッドの体積です aピラミッドの底辺 hピラミッドの高さ 正四角錐の体積 正四角錐底面が正方形で、二等辺三角形に等しいピラミッド。正四角錐の体積（底辺と高さから） 答えを知れて良かったが、途中式が分からないので、あまり勉強にはならなかった。 a=8,h=3にすると体積がになります。 (14桁の場合) 正しくは、64です。 修正お願いいたします。 失礼致しました。 ご指摘

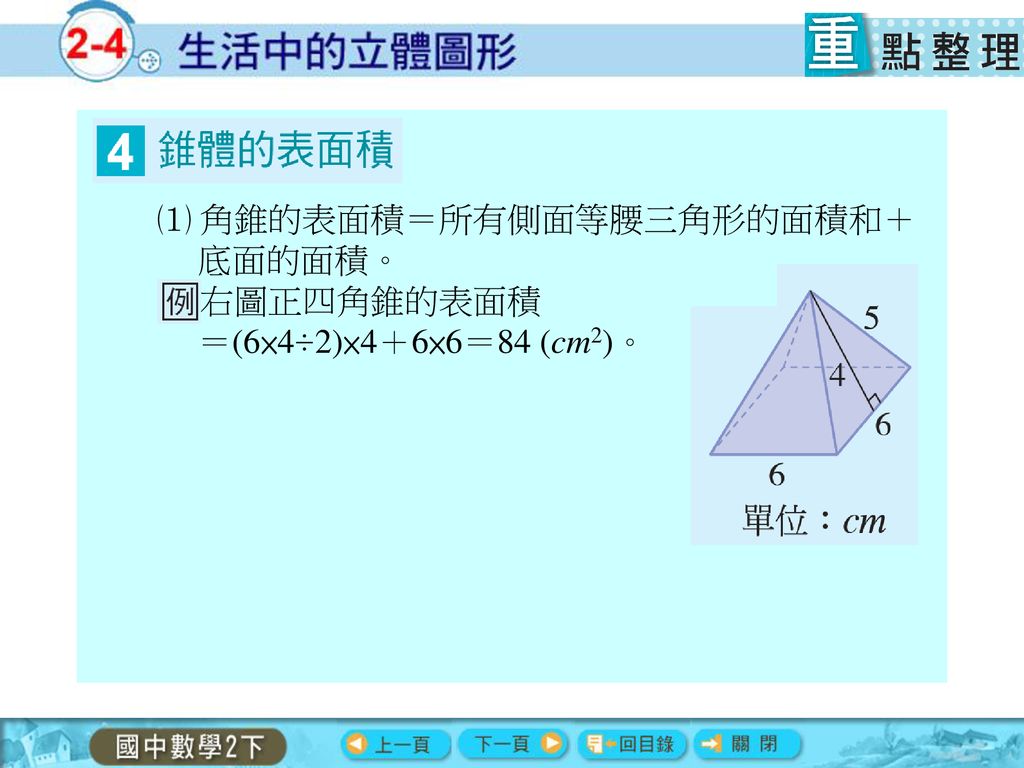
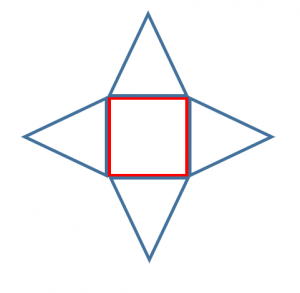
四角錐の表面積の求め方 公式 小学生 中学生の勉強

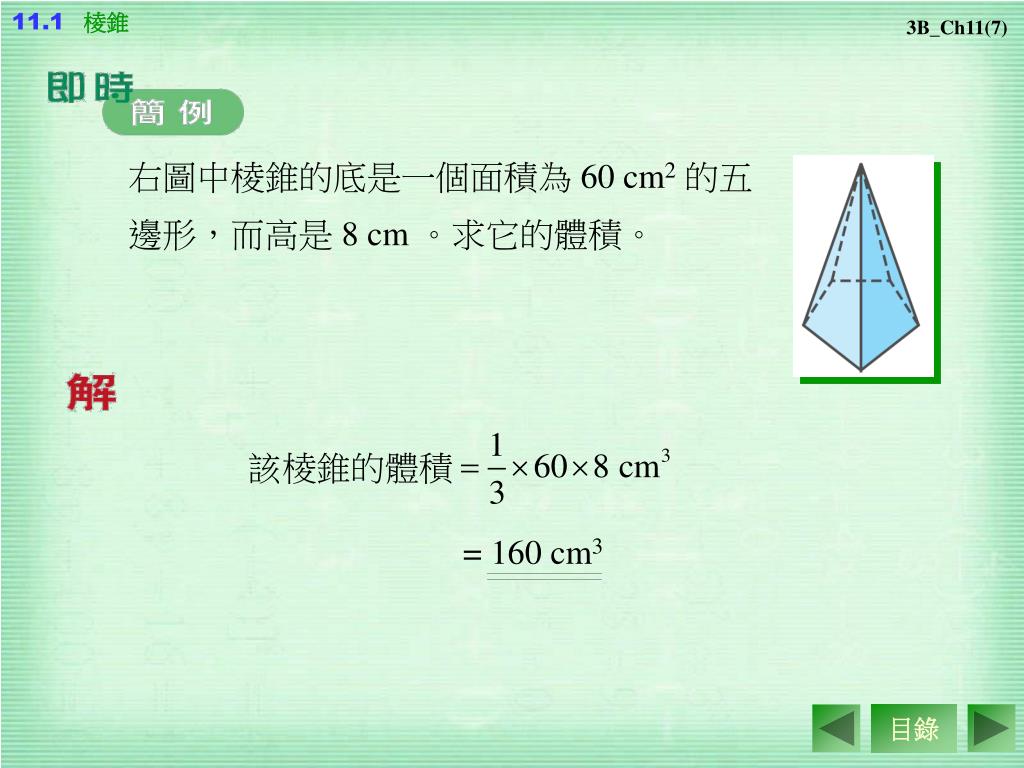
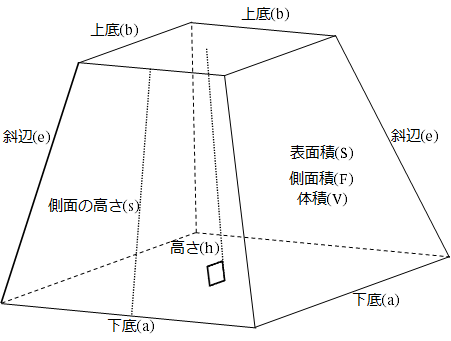
体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。 このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう！四角錐台の体積を計算する必要がありました。 上記公式に数字を当てはめるとA＝43 B＝36 a＝29 b＝19 h＝18 単位cmです。 公式に当てはめて計算してみると大方18リットル＝10升＝?斗であることがわかりました。要点四角錐，三角錐，円錐の体積 三角錐，四角錐，円錐の体積 V は，それがちょうど入る四角柱，三角柱，円柱の体積の です． 特に，円錐については，底面の半径が r であるとき，底面積が S=πr 2 と書けるから と書くこともできます．

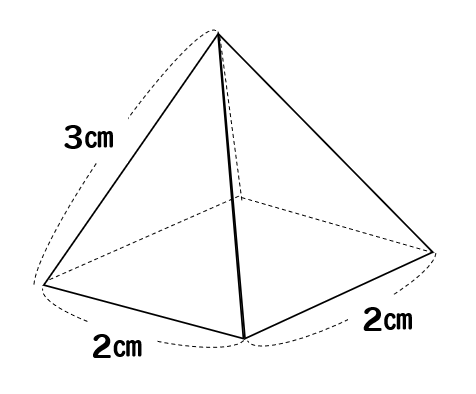
三角錐でも良いが、すべての面が合同な正三角形なので正四面体が最も適切である。 (2) 正四面体acfhの体積を直接出すことは無理なので、 立方体から、いらない部分を引き算して求める。 いらない部分は全て同じ形の三角錐である。 1 1 回答 辺の長さが全て6cmの正四角錐の体積と表面積を教えてください！ わかりやすい解説を込みで即回答お願いします！ 辺の長さが全て6cmの正四角錐の体積と表面積を教えてください！ わかりやすい解説を込みで即回答お願いします！ 続きを読む右の図の正四角錐の体積と表面積を求めよ。 解 底面積は，10 =100 cm より， 体積は， 1 3 ×100×12=400 (cm3) 側面積は， 1 2 ×10×13 ×4=260 cm より， 表面積は，=360 (cm2) 160 次の角錐の体積を求めよ。また，⑶については表面積も求めよ。

正四 角錐 体積のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

四角錐 Wikiwand	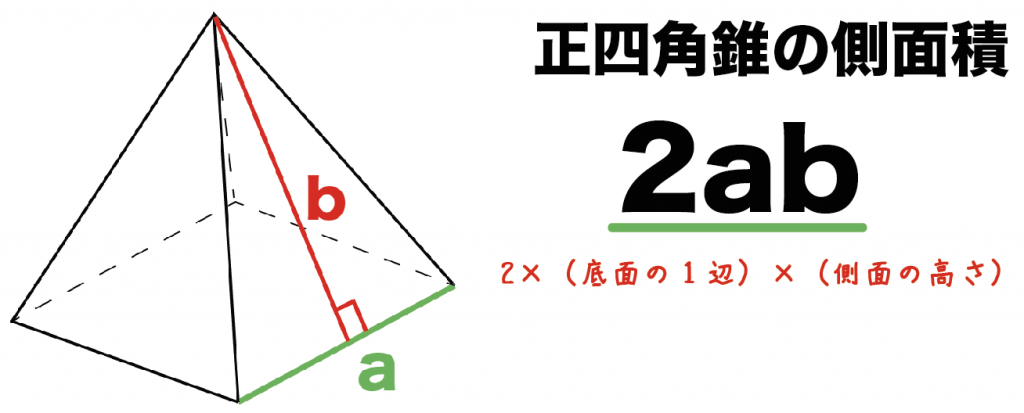四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	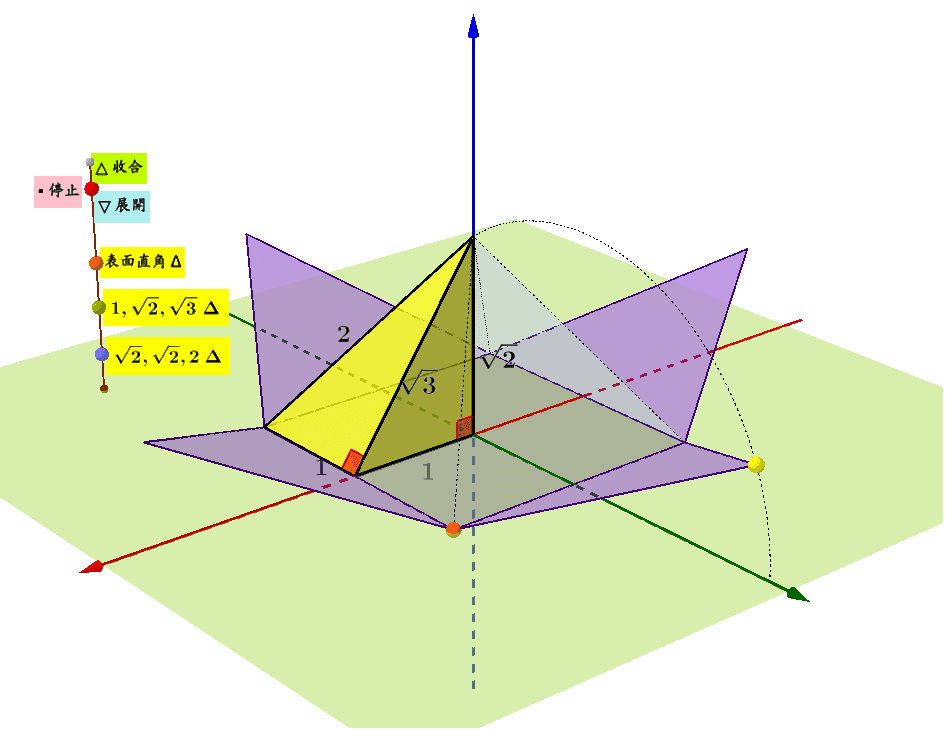四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	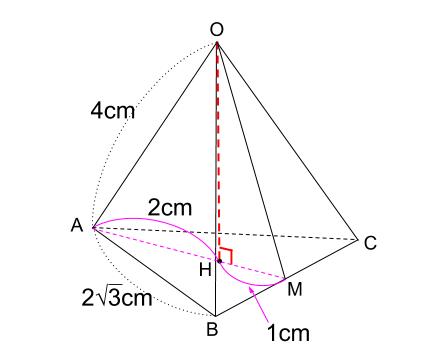四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	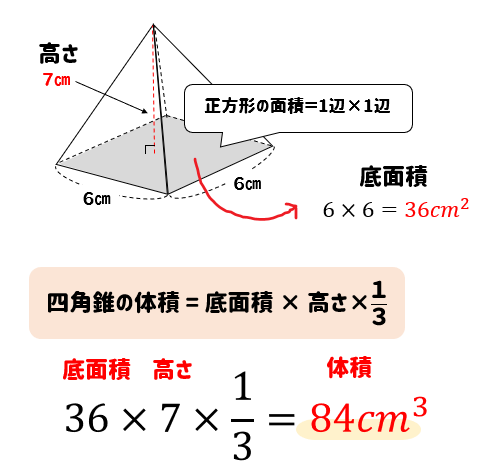四角錐 Wikiwand
四角錐 Wikiwand	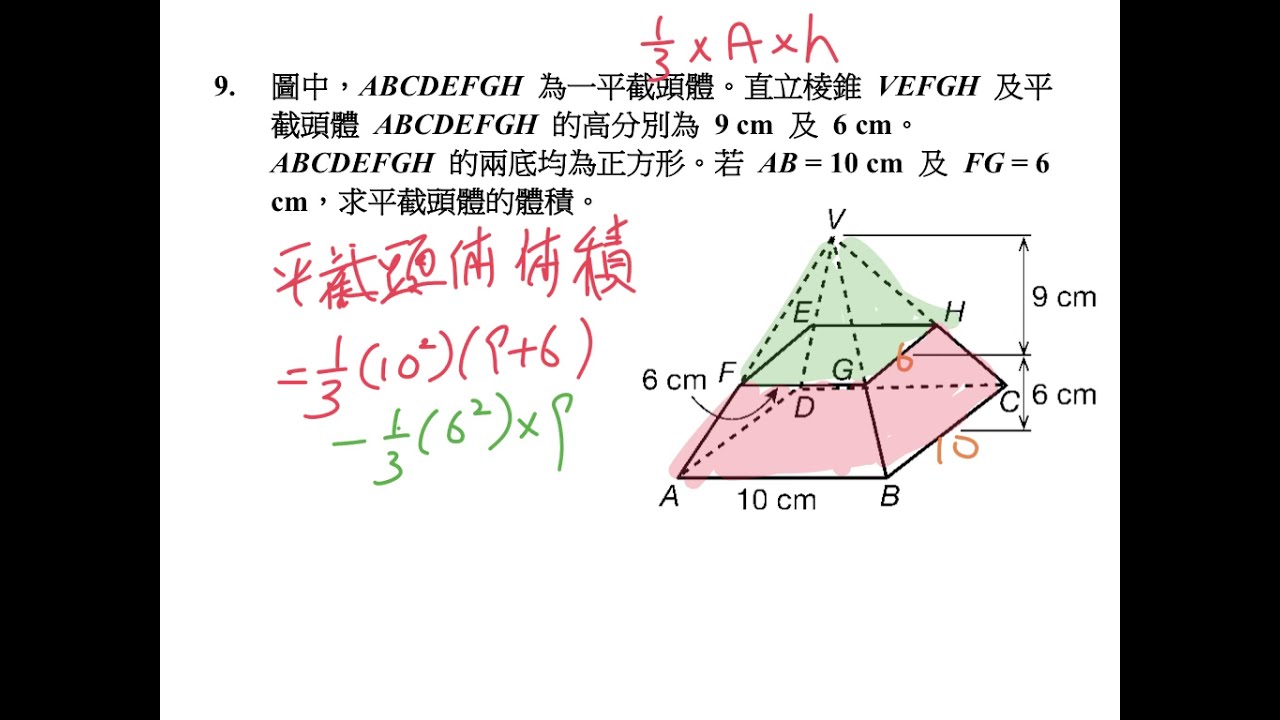四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	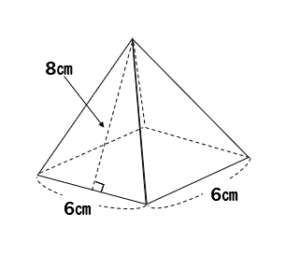四角錐 Wikiwand
四角錐 Wikiwand	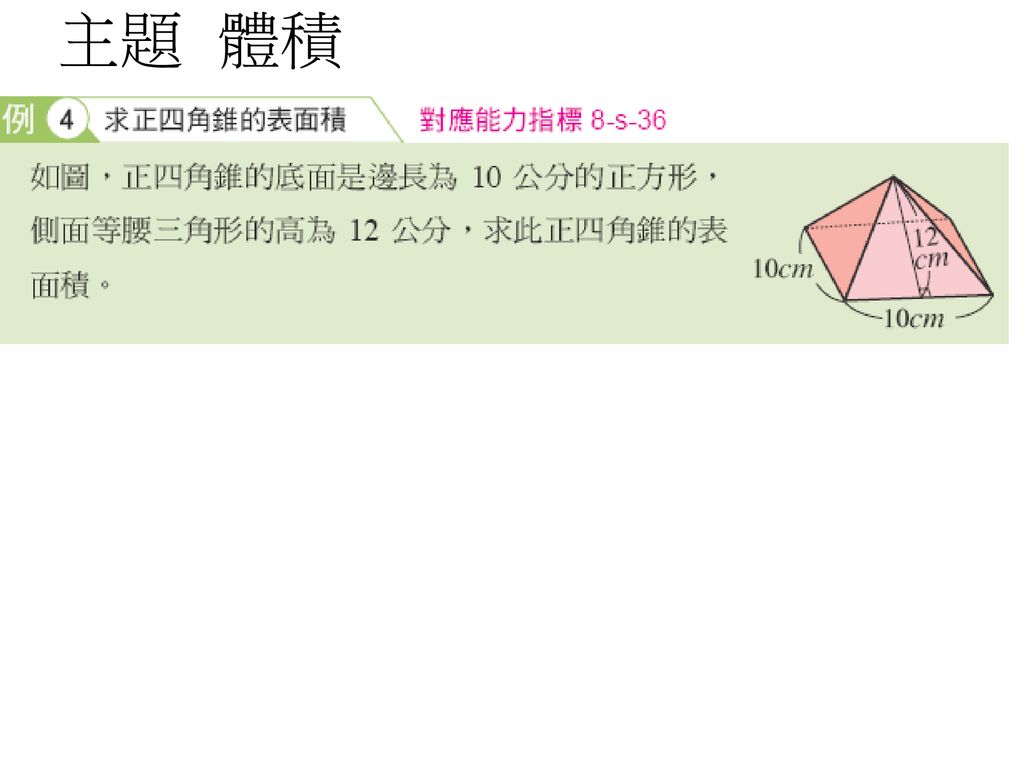四角錐 Wikiwand	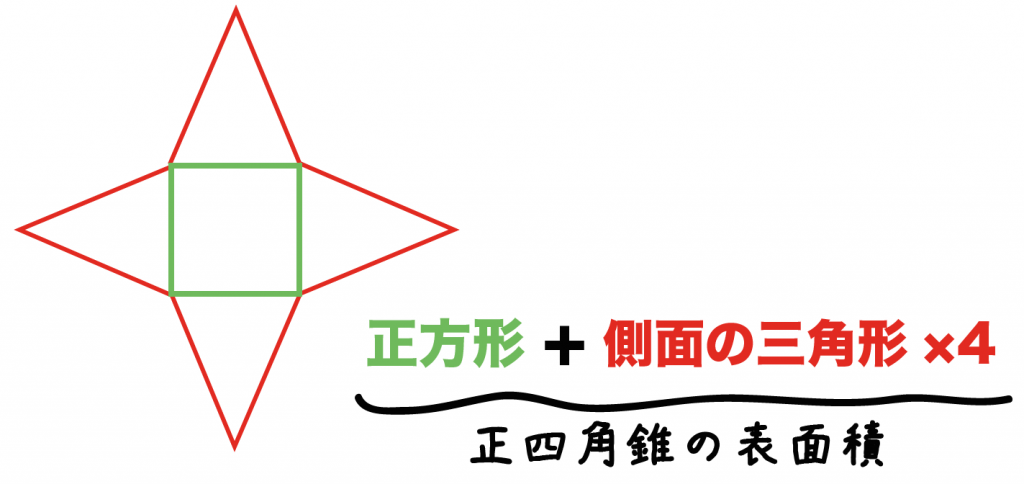四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	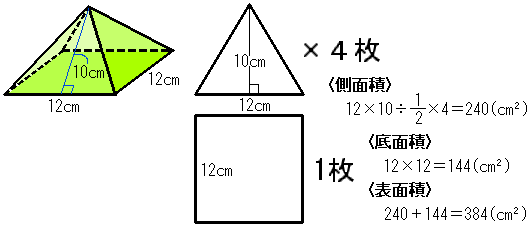四角錐 Wikiwand	四角錐 Wikiwand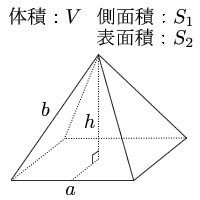
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand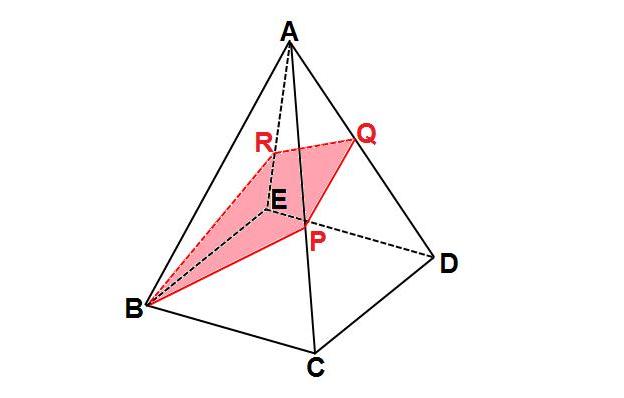
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	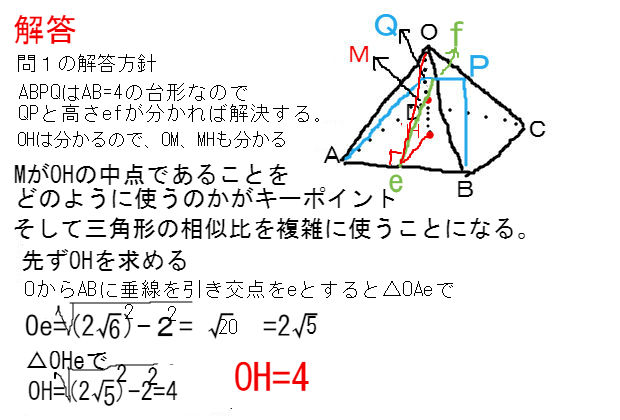四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand
四角錐 Wikiwand	四角錐 Wikiwand	四角錐 Wikiwand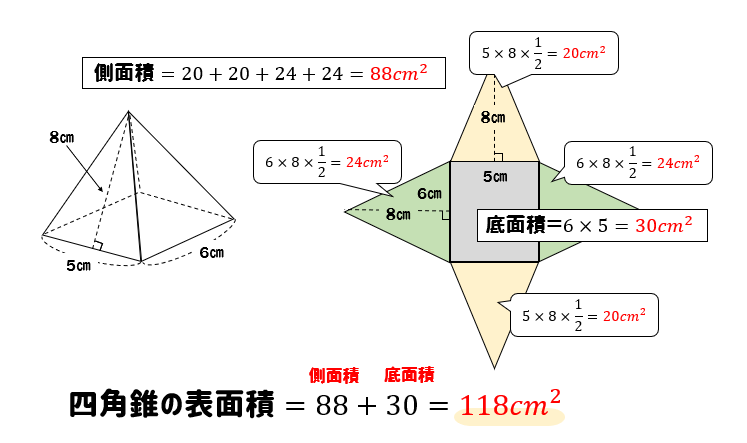
四角錐 Wikiwand	四角錐 Wikiwand

 特殊な四角錐の場合 底面が一辺 2 h 2h 2 h の正方形であるような特殊な正四角錐の場合は，立方体を六個に切ることで簡単に V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h が証明できます。 錐体（円錐、角錐）の体積は、底面積が S S 、高さが h h の錐体の体積 V V は以下の式で表します。 V = 1 3Sh V = 1 3 S h この公式を学習したときに 1 3 1 3 になる理由は知らなかったと思います。 これは特殊な四角錐の場合には比を用いて簡単に証明することが